Генетические алгоритмы

Строительные блоки (Building blocks)

Группа исследований эволюционных алгоритмов (ТПУ)

Дискуссионная группа по эволюционным вычислениям

Написать письмо

Строили мы, строили и, наконец, построили.
Э.Успенский, "Чебурашка"

Строительный блок (СБ) (building block (BB)) - это одно из ключевых понятий в теории генетических алгоритмов, наряду с шаблоном (шимой) и теоремой шаблонов (теоремой шим). К строительным блокам (как правило) принято относить шаблоны с малой определяющей длиной, малым порядком и высокой приспособленностью. Приспособленность СБ чаще всего определяется как средняя приспособленность особей, хромосомы которых содержат данный строительный блок.

В гипотезе о строительных блоках (building blocks hypothesis) считается, что в процессе работы генетического алгоритма, по мере приближения к глобальному оптимуму, порядок и приспособленность строительного блока увеличиваются. Т.е. в начале эволюции относительно высокой приспособленностью обладают строительные блоки малой определяющей длины, затем, в результате отбора и рекомбинации, появляются более приспособленные и "длинные" строительные блоки. Таким образом, говорят об обработке строительных блоков (building blocks processing) в результате работы генетического алгоритма.

Выделяют следующие проблемы в обработке строительных блоков:
1. Идентификация.
2. Смешивание.

Под идентификацией понимается проблема нахождения (локализации) строительного блока. Иными словами, какой именно участок хромосомы можно считать строительным блоком. Очевидно, что минимальный по размерам СБ представляет один разряд, а максимальный - всю хромосому. Но это в простейшем варианте, а в случае "не граничных условий" количество "претендентов" на гордое звание строительного блока очень велико. В частности, для хромосомы длины n может существовать С(n, 2) различных позиций для строительных блоков 2-го порядка, С(n, 3) различных позиций для строительных блоков третьего порядка и т.д., где C(n, m) - количество сочетаний из n по m (вычисляется как n!/(m!(n-m)!), где "!" - факториал, т.е. n! = 1*2*...*(n-1)*n, где "*" - обозначает операцию умножения, 1, 2 и иже с ними - арабские цифры (есть еще и римские, но их рассмотрение выходит за рамки выбранной для данной статьи темы)).

Проблема смешивания заключается в том, что, даже если строительные блоки найдены, трудно определить, какие из них стоит смешивать (грубо говоря, помещать в одну хромосому), а какие - нет. Т.к. высокая приспособленность различных строительных блоков не гарантирует высокой приспособленности хромосом, полученных в результате их комбинации. Например, рыцарские латы хорошо защищают от ударов и комаров, танк в этом отношении еще лучше, но рыцарь в танке, согласитесь, смотрится нелепо, не говоря уж о том, что управлять танком он вряд ли сможет, т.к. развернуться там особенно негде, и подлые комары над рыцарем еще надругаются (и чует сердце, что неоднократно).

В силу обозначенных проблем уделяется довольно много внимания разработке операторов и подходов, которые позволили бы обеспечить эффективную (BB-wise) обработку строительных блоков. Также есть мнение, что эффективная идентификация и смешивание являются критическими условиями для обеспечения успешной работы генетического алгоритма.

Помимо идентификации и смешивания существует проблема неопределенности приспособленности строительного блока (building block fitness noise). Поскольку один и тот же строительный блок может входить как в хорошие (с точки зрения решаемой задачи) хромосомы, так и в не очень, то приспособленность этого строительного блока практически всегда определяется с некоторым "шумом". Это осложняет задачу выбора между двумя строительными блоками, т.к. даже если приспособленность одного из них выше, чем приспособленность другого, всегда есть вероятность сделать неправильный выбор. Говоря по-другому, в результате селекции может быть выбрана особь с менее приспособленным строительным блоком. Графически это можно представить следующим образом (рис.1) (Goldberg D.E., Deb K., Clark J.H. Genetic Algorithms, Noise, and the Sizing of Populations, 1991).

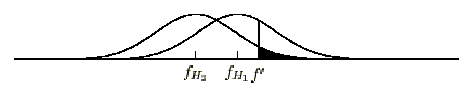
Рис.1

Пусть H1 и H2 два строительных блока, приспособленности которых распределены по нормальному закону, причем f_H1 и f_H2 соответственно средние приспособленности блоков 1 и 2. Пусть также приспособленность H1 больше, чем приспособленность Н2. Если имеется небольшое число хромосом, содержащих рассматриваемые блоки, то их приспособленности определены с достаточно большой погрешностью, иными словами, дисперсия распределений велика. Таким образом, площадь взаимного "наложения" распределений также значительна, и, следовательно, значительна вероятность выбрать в результате селекции менее приспособленный строительный блок. В случае, представленном на рис.1, вероятность выбрать хромосому с приспособленностью больше f' и содержащую шаблон Н2, равна площади закрашенной части распределения приспособленности 2-го шаблона.

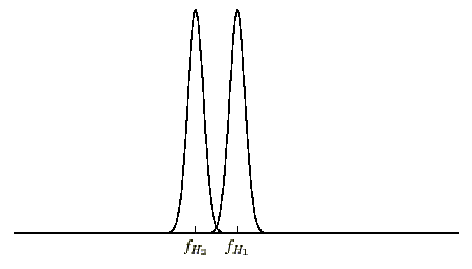
Рис.2

Если увеличить количество хромосом содержащих рассматриваемые строительные блоки (например, увеличив размер популяции), то тогда распределения приспособленностей обоих блоков "сжимаются", т.к. значения приспособленностей определяются более точно (рис.2). Тем самым уменьшается вероятность выбора менее приспособленного строительного блока.

Несмотря на то, что изначально строительные блоки определялись как шаблоны с определенными свойствами, т.е. применительно к ГА с бинарным кодированием, аналоги шаблонов, а следовательно и строительных блоков, можно найти и в других видах эволюционных вычислений (не только в генетических алгоритмах). На мой взгляд, концепция строительных блоков давно уже живет "своей жизнью", отдельно от теоремы шаблонов, т.к. за СБ можно считать любой участок хромосомы определенного вида вне зависимости от того, возможно ли описание хромосом, содержащих этот блок, одним шаблоном или нельзя. Наибольшее внимание вопросу изучения строительных блоков уделяется в Лаборатории генетических алгоритмов в Иллинойсе (Illinois Genetic Algorithms Laboratory - IlliGAL), под руководством Дэвида Голдберга (David Goldberg).

Источники:

1. Deb, K. Genetic algorithms in search and optimization: The technique and applications. // Proceedings of International Workshop on Soft Computing and Intelligent Systems. - Calcutta, India: Machine Intelligence Unit, Indian Statistical Institute, 1998. - P.58-87.
2. Goldberg D.E., Deb K., Clark J.H. Genetic Algorithms, Noise, and the Sizing of Populations. IlliGAL Report No. 91010. - University of Illinois, Urbana-Champaign, 1991.
3. Sastry K. Analysis of Mixing in Genetic Algorithms: A Survey. IlliGAL report No.2002012. . - University of Illinois, Urbana-Champaign, 2002.
4. Исаев С.А. Генетические алгоритмы - эволюционные методы поиска.

[11 февраля 2005г.]