Генетические алгоритмы

Шаблоны и теорема шаблонов

Группа исследований эволюционных алгоритмов (ТПУ)

Дискуссионная группа по эволюционным вычислениям

Написать письмо

Шаблон (schema, шима)

Понятие шаблона было введено Холландом и используется для анализа работы ГА. В частности рассматриваются процессы конструирования и разрушения определенного шаблона в течение развития популяции (schema dynamics).

Шаблоном называется строка вида

Символом "*" в некотором разряде обозначается то, что там может быть как 1, так и 0. Например, для двух бинарных строк "111000111000" и "110011001100" шаблон будет выглядеть следующим образом: "11*0****1*00". Т.е. с помощью шаблонов можно как бы выделять общие участки двоичных строк и маскИровать различия. Имея в составе шаблона m символов "*" можно закодировать (обобщить) 2^m двоичных строк. Так, например, шаблон "01*0*1" описывает набор строк

Опеределяющей длиной шаблона (schema defining length) называется расстояние между двумя крайними символами "0" и/или "1". Для шаблона "01*0*1" определяющая длина равна 5, а для шаблона "**0**1*" определяющая длина равна 3. Порядок шаблона (schema order) - это ещё одна характеристика шаблона и равна она числу фиксированных позиций в строке, т.е. общему числу "0" и "1". Для шаблонов "01*0*1" и "**0**1*" порядки равны 4 и 2 соответственно.

Теперь о том, какое отношение шаблон имеет к генетическим алгоритмам. Дело в том, что хромосома, по сути, является двоичной строкой. В то же время особи, которой принадлежит хромосома, содержащая набор генов-параметров задачи, поставлена в соответствие величина, характеризующая её приспособленность. Т.к. шаблон является обобщением нескольких бинарных строк (хромосом), то можно говорить, что особи, обладающие хромосомами, которые соответствуют одному шаблону более приспособленны, а особи с хромосомами, соответствующими другому шаблону - менее приспособлены.

Далее. Можно сказать, что смысл работы ГА заключается в поиске двоичной строки определенного вида из всего множества бинарных строк. Пространство поиска составляет 2^L строк, а его мерность равна L (L-мерное пространство), где L - длина хромосомы. Шаблон соответствует некоторой гиперплоскости в этом пространстве. Данное утверждение можно проиллюстрировать следующим образом. Пусть разрядность хромосомы равна 3, тогда всего можно закодировать 2³=8 строк. Представим куб в 3-мерном пространстве. Обозначим вершины этого куба 3-разрядными бинарными строками так, чтобы метки соседних вершин отличались ровно на один разряд, причем вершина с меткой "000" находилась бы в начале координат. Вариант обозначения можно изображен на рис.1.

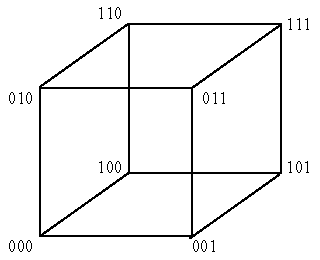
Рис.1. 3-мерный куб

Если взять шаблон вида "**0", то он опишет левую грань куба, а шаблон "*10" - верхнее ребро этой грани. Очевидно, что шаблон "***" соответствует всему пространству. Если взять двоичные строки длиной 4 разряда, то разбиение пространства шаблонами можно изобразить на примере 4-мерного куба с поименованными вершинами (рис.2).

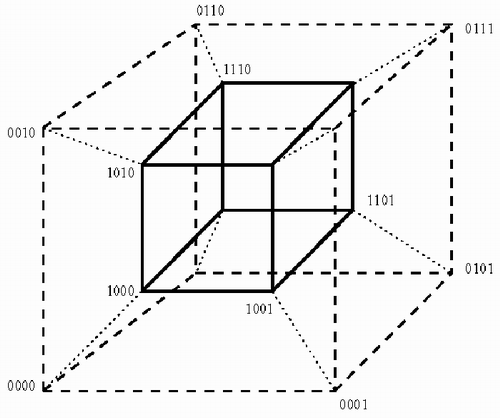
Рис.2. 4-мерный куб

Здесь шаблону "*1**" соответствует гиперплоскость, включающая задние грани внешнего и внутреннего куба, а шаблону "**10" - гиперплоскость с верхними ребрами левых граней обоих кубов.

Разбиение пространства поиска можно представить и по другому. Представим координатную плоскость, в которой по одной оси мы будем откладывать значения двоичных строк, а по другой - значение целевой функции (рис.3).

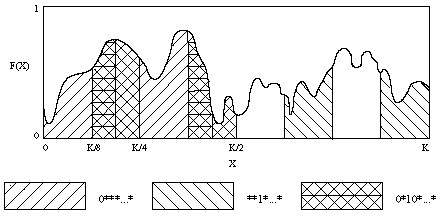
Рис.3. Разбиение пространства

Участки пространства, заштрихованные разным стилем, соответствуют разным шаблонам. Число К в правой части горизонтальной оси соответствует максимальному значению бинарной строки - "111...111". Из рисунка видно, что шаблон "0***...*" покрывает всю левую половину отрезка, шаблон "**1*...*" - 4 участка шириной в одну восьмую часть, а шаблон "0*10*...*" - левые половины участков, которые находятся на пересечении первых двух шаблонов. Таким образом и происходит разбиение пространства в этом случае.

Теорема шаблонов (The schema theorem, теорема шим)

Теорема шаблонов является одной из основных теорем теории ГА. Сразу отмечу, что данная теорема была получена для канонического ГА и по отношению к другим вариантам ГА, реализующим отличные от канонического стратегии отбора и формирования нового поколения, практически бесполезна.

С развитием теории ГА теорема шаблонов претерпевала незначительные изменения и поправки. Ниже я приведу первоначальный вариант теоремы шаблонов 1975г. и исправленный вариант 1992г. Обе эти теоремы принадлежат Д.Холланду. Есть ещё так называемая точная теорема шаблонов, авторство по-моему принадлежит Голдбергу, но я её пока не нашел (или плохо искал ;)).

Для начала представим, что у нас есть популяция двоичных строк длины L. Я нарочно не говорю о хромосомах и генах, чтобы облегчить восприятие. Вероятность проведения кроссовера равна Р_с. Тип кроссовера: одноточечный. Пусть определяющая длина шаблона Н равна d(Н), а его приспособленность f(H). Доля строк, соответствующих шаблону Н в текущем поколении T, равна m(H,t). Нас интересует, какая доля строк, соответствующих шаблону Н будет присутствовать в популяции в следующем поколении - m(H,t+1).

Прежде чем идти дальше, остановимся на одном моменте, а именно, с какой вероятностью кроссовер разрушит уже имеющийся шаблон. Очевидно, что если точка разрыва не попадает внутрь уже имеющегося шаблона, то шаблон не будет разрушена. Т.е. если Р_с*d(Н)/(L-1) - вероятность того, что точка разрыва попадет внутрь шаблона, то 1-Р_с*d(Н)/(L-1) - вероятность того, что кроссовер не разрушит шаблон.

Согласно стратегии отбора канонического ГА шансы особи принять участие в скрещивании вычисляются в соответствии с отношением f/f_ср, где f - значение приспособленности данной особи, а f_ср - средняя приспособленность. Таким образом, вероятность того, что строка соответствующая шаблону Н будет участвовать в скрещивании равна m(H,t)*f(H,t)/f_ср(t). Принимая во внимание вероятность разрушения шаблона кроссовером, можно сформулировать первоначальную теорему шаблонов (Холланд, 1975):

Рис.4. Теорема шаблонов (1975г.)

Одним из недостатков данной теоремы является то, что в ней отсутствует влияние мутации на создание и разрушение шаблонов. Если считать, что вероятность мутации одного разряда равна P_m, а порядок шаблона Н равен о(Н), то вероятность того, что мутация не разрушит шаблон равна (1-P_m)^o(H). Т.е. если мутирующий разряд не попадает ни на одну фиксированную позицию внутри шаблона, то она не изменяется. С учетом этого исправленная теорема шаблонов выглядит следующим образом (Холланд, 1992):

Рис.5. Исправленная теорема шаблонов (1992г.)

Теперь немного критики. Как уже было отмечено, классическая теорема шаблонов неприминима к ГА, модели, которых отличаются от канонического ГА. Кроме этого в теореме шаблонов практически не учитывается то обстоятельство, что кроссовер и мутация могут не только разрушать шаблон, но создавать её из других шаблонов. Поэтому в теореме шаблонов присутствует знак неравенства. Ещё одним недостатком теоремы шаблонов является то, что она позволяет рассчитать долю шаблонов в популяции только для следующего поколения. Т.е. при попытке подсчитать число строк, соответствующих данному шаблону через несколько поколений с использованием теоремы шаблонов к успеху не приведет. Так получается, в частности, из-за пропорциональной стратегии отбора.

Однако приведенные аргументы не умаляют значение теоремы шаблонов. Это была, наверное, первая серьёзная, а главное, успешная попытка понять, как и почему работают ГА. Сама же теория шаблонов является на сегодняшний день одним их самым распространенных инструментов анализа ГА.

Источники:

1. Robin Biesbroek "Genetic Algorithm Tutorial. 4.1 Mathematical foundations", 1999
2. David E. Goldberg, Kumara Sastry "A Practical Schema Theorem for Genetic Algorithm Design and Tuning", 2001.
3. Darrel Whitley "A Genetic Algorithm Tutorial", 1993.
4. Исаев С.А. "Генетические алгоритмы - эволюционные методы поиска".