Генетические алгоритмы
Тестовые функции
| На главную |
| Генетические алгоритмы |
| Группа исследований эволюционных алгоритмов (ТПУ) |
| Дискуссионная группа по эволюционным вычислениям |
| Написать письмо |
Итак вы написали свой собственный ГА и теперь вам хочется знать насколько он хорош. Ниже приведены некоторые тестовые функции для ГА, которые я нашел в сети на странице Лазаускаса, адрес не помню, но помню, что вышел туда с личной страницы В.Спирса. Также я находил тестовые функции, которые предлагает Де Йонг (один из студентов Холланда), их я буду помечать DeJong1, DeJong2, DeJong3, DeJong4 и DeJong5 в соответствии с тем, как он их пронумеровал.
Все тестовые функции могут иметь различное число параметров (n). Поэтому имеет смысл запустить алгоритм для оптимизации некоторой функции сначала с небольшим n (например, 10 или 20), а затем с n=50, 100, 200,... Это даст возможность проверить масштабируемость алгоритма.
Эффективность работы ГА принято оценивать количеством вычислений целевой функции. Чем меньше, тем лучше. После некоторых функций приведены результаты работы моего ГА (назовем его QGA). Сразу оговорюсь, что результаты целевой функции меньше 0.001 тоже засчитывались как найденный глобальный минимум. Вот характеристики QGA:
- Фиксированный размер популяции;
- Фиксированная разрядность генов;
Количество точек разрыва кроссовера равно числу генов (на каждый ген приходится ровно одна точка);
- Для скрещивания отбираются 50% популяции;
- Вероятность мутации 95%;
- Две "элитные" особи;
- Удаление одинаковых особей из популяции (с помощью мутации);
- Точность вычислений: 0.001;
- Результат подсчитан по 50 запускам алгоритма;
Т.к. генетические алгоритмы используют стохастичность, то для того, чтобы определить, насколько эффективен ваш ГА нужно запустить его на одной и той же тестовой функции несколько раз и только после этого анализировать результат. Например, мой ГА для функции Растригина от 50 переменных находит глобальный минимум в ~40% случаев, используя не более 10000 вычислений функции.
Для некоторых функций есть графики для случая двух переменных. Графики представляют "сечение" поверхности функции плоскостью, проходящей через глобальный минимум, перпендикулярной одной из осей координат.
Базовый набор тестовых функций для бинарных и вещественных способов кодирования, многокритериальной оптимизации и генетического программирования приведен в переводе раздела "11.2 Простые тестовые задачи" из книги Luke S. Essentials of Metaheuristics. A Set of Undergraduate Lecture Notes. Zeroth Edition. Online Version 0.2. September, 2009 (http://cs.gmu.edu/~sean/book/metaheuristics/). Обратите внимание, набор далеко неполный и если вы хотите замучить свой алгоритм по-настоящему гуглите по фразе "rotated and ridge functions".
Также большой набор тестовых функций есть здесь.
Если что, можете присылать свои результаты, я их также размещу для сравнения, а также для увеселения публики :)).
Считается легкой функцией для любого метода оптимизации.
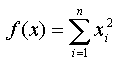
хО(-5,12; 5,12)
Один минимум равный 0 в точке, где xi=0.0.
Результат QGA:
n=10, количество нахождений глобального минимума (вообще-то он здесь один...:)) 86%,
число вычислений целевой функции не более 1250, максимальное значение 0,008325.
n=30, количество нахождений глобального минимума 34%, число вычислений целевой
функции не более 1250, максимальное значение 0,108851.
n=50, количество нахождений глобального минимума 46%, число вычислений целевой
функции не более 2500, максимальное значение 0,016291, для скрещивания отбиралось
40% популяции.
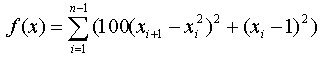
хО(-2,048; 2,048)
Минимум равный 0 в точке, где xi=1.0.
Функция имеет большое медленно убывающее плато.
Результат QGA:
n=2, количество нахождений глобального минимума 92%, число вычислений целевой
функции не более 1250, максимальное значение функции 0,00169118.
n=4, количество нахождений глобального минимума 86%, число вычислений целевой
функции не более 1250, максимальное значение функции 0,00504982.
n=10, количество нахождений глобального минимума 0%, число вычислений целевой
функции не более 10000, максимальное значение функции 0,0186537, минимальное значение
функции 0,0019092, для скрещивания отбиралось 50% популяции.
n=10, количество нахождений глобального минимума 8%, число вычислений целевой
функции не более 10000, максимальное значение функции 0,0127758, для скрещивания отбиралось
40% популяции.
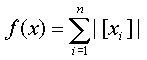
хО(-5,12; 5,12)
|[xi]| - модуль целой части
Минимум равный 0 в точке, где xi=0.0.
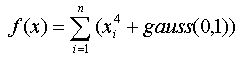
хО(-1.28; 1.28)
gauss(0,1) - функция, возвращающая случайную величину с нормальным распределением с мат.
ожиданием в 0 и дисперсией равной 1.
Минимум равный 0 в точке, где xi=0.0.
Пока что нету, т.к. я встретил несколько вариантов и не "въехал", что - куда.
Функция со сложным рельефом. Считается сложной для оптимизации.
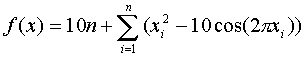
хО(-5,12; 5,12)
Минимум равный 0 в точке, где xi=0.0.
Локальный минимум в точке, где одна координата равна 1.0, а остальные равны 0.0
Результат QGA:
n=20, количество нахождений глобального
минимума 16%, число вычислений целевой функции не более 5000, максимальное
значение функции 19,8992.
n=20, количество нахождений глобального минимума 26%, число вычислений целевой
функции не более 10000, максимальное значение функции 17,997.
n=50, количество нахождений глобального минимума 38%, число вычислений целевой
функции не более 10000, максимальное значение функции 49,869.
Возможно, такие странные результаты обусловленны рельефом функции Растригина от 20 и 50
переменных, а может быть, и работой моего ГА. Например, мне никак не удается
точно аппроксимировать квадратичной функцией (всего-то три параметра) набор из пяти точек, которые строго
принадлежат графику параболы.>:-i
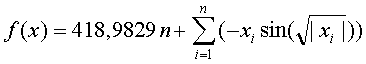
хО(-500; 500)
Минимум равный 0 в точке, где xi=420.9687.
Локальный минимум в точке, где одна координата равна -302.5232, а остальные равны 420.9687.
Т.к. локальный минимум находится далеко от глобального, то есть опасность, что алгоритм
"собъется с пути".
Угол под знаком синуса получается в радианах.
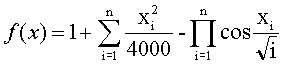
хО(-600; 600)
Минимум равный 0 в точке, где xi=0.0.
При n=10 есть ещё 4 локальных минимума равных 0,0074 приблизительно в точке
(+-Pi, +-Pi*sqrt(2), 0, ..., 0).
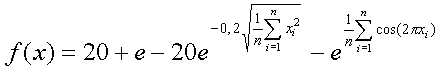
хО(-30; 30)
Минимум равный 0 в точке, где xi=0.0.
Источники:
Deniz Yuret and Michael de la Maza "Dynamic Hill Climbing: Overcoming the limitations of optimization techniques.".
Тестовые функции с личной страницы Вильяма Спирса (William Spears)